


Localidad: Longitud: Latitud: Altura:
El geoide es la superficie suave pero irregular que tendrían los océanos contemplando como causas solamente a la gravedad y la rotación terrestre, y más o menos, se corresponde con lo que llamamos usualmente "el nivel del mar". La normal al geoide coincide con la dirección de la plomada. Se define el ecuador instantáneo como el plano que pasa por el centro de masas de la Tierra (geocentro) y es ortogonal al eje instantáneo de rotación. En cada punto del geoide, el ángulo que forman la normal y el ecuador instantáneo se llama latitud astronómica. El problema aquí, es que el geoide es una superficie muy complicada para su aplicación matemática, y normalmente, se adopta como superficie teórica de la Tierra un elipsoide de revolución, tratando que se adapte lo máximo posible al geoide. El elipsoide se encontrará unas veces sobre el geoide y otras por debajo. Esto da lugar a los llamados sistemas de referencia geodésicos. Dentro de estos cabe distinguir los sistemas locales, que utilizan para su definición un elipsoide determinado y un punto datum, y los sistemas globales cuyos parámetros están dados por una terna rectangular (X, Y, Z) cuyo origen se encuentra en el geocentro terrestre. El plano que pasa por el centro del elipsoide y es ortogonal a su eje se llama ecuador medio. En cada punto del elipsoide, el ángulo que forman la normal y el ecuador medio se llama latitud geodésica. Las latitudes astronómicas y geodésicas difieren muy poco entre si.
El GPS se basa en el sistema de referencia geodésico global WGS84. Este esta definido por un elipsoide de revolución cuyo origen coincide con el geocentro, utiliza como eje Z el polo IERS y como eje X el meridiano 0 definido por el IERS. El eje Y completa el sistema formando una tripleta dextrógira. Se utiliza como referencia para obtener coordenadas geográficas del siguiente modo: dado un punto P (por ejemplo la cima del Monte Everest), si se traza la normal Ne al elipsoide que pasa por P, el ángulo que forma Ne con el plano del ecuador nos da la latitud (geodésica) de P, y el ángulo que forma el plano del meridiano que pasa por P y el plano del meridiano origen nos da la longitud de P. La altura elipsoidal o geodésica de P es la distancia de P al elipsoide medida sobre Ne. Si por P, ahora trazamos una normal Ng al geoide, la distancia de P al geoide medida sobre Ng se llama altura ortométrica de P. Las diferencia entre la altura elipsoidal y ortométrica se llama altura geoidal. Alcanza un valor mínimo de -107 metros y un valor máximo de 86 metros.
Para ver esto con un poco más de detalle, supongamos que para una posición geográfica dada, h es la altura elipsoidal, y H la altura ortométrica. Entonces la diferencia N=h-H es la altura geoidal. Si N > 0, el elipsoide esta por debajo del geoide, mientras que si N > 0 ocurre lo contrario:
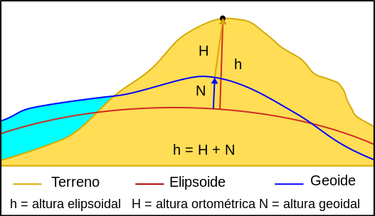
El sistema GPS nos proporciona la altura elipsoidal h. Para conocer la altura ortométrica H (que nos resulta más familiar pues se refiere al nivel del mar y no a un elipsoide imaginario), es necesario saber cual es la altura geoidal N, ya que H=h-N. Para ello hace falta un modelo gravimétrico de la Tierra (o EGM por sus siglas en inglés). Estos dan una expresión del potencial gravitatorio de la Tierra, y modelan el geoide como una de sus superficies equipotenciales. Al referir esa superficie al elipsoide WGS 84 obtenemos la altura geoidal (que en realidad es la altura geodésica del geoide). EGM96 es uno de tales modelos y EGM2008 es otro más reciente y preciso. En internet hay varios sitios que permiten calcular la altura geoidal para una posición geográfica dada:
www.unavco.org/software/geodetic-utilities/geoid-height-calculator/geoid-height-calculator.html